广告 | 点击查看

摘要：随着重载物流的快速发展，超重载堆垛机在仓储系统中的作用日益重要。然而，超重载堆垛机在运行过程中存在效率与立柱振幅之间的矛盾：提高运行速度会加剧振动，而降低振幅可能导致作业效率降低。为了解决这一问题，本文提出了一种基于遗传算法的超重载堆垛机运行效率与振幅协同优化方法。首先，根据堆垛机质量分布情况建立立柱顶端动态挠度方程，并考虑载货台高度变化的影响；其次，推导立柱顶端振动方程并构建Simulink仿真模型，通过对比两种典型速度控制曲线的仿真结果，确定最优水平速度控制曲线；最后，采用遗传算法优化水平与垂直运动的协同策略，综合考虑运行效率与稳定性。实验结果表明，该方法显著降低了立柱振幅，同时保证了作业效率。本文的研究为超重载堆垛机的性能优化提供了理论支持，为重载物流场景下的高效、精准作业提供了解决思路。

关键词：超重载堆垛机；遗传算法；协同优化；立柱振幅

作者：张浩1 刘向东2 朱岩2 刘园园2 马荣路2

1中国机械科学研究总院有限公司

2北自所（北京）科技发展股份有限公司

一

引言

随着重载物流的快速发展，仓储系统对堆垛机的性能提出了更高要求。重载堆垛机作为重载物流系统核心设备，不仅需要具备强大的承载能力，还需在高速运行过程中保持高精度和稳定性，以确保货物的安全运输和系统的高效运作。然而，重载堆垛机在实际运行中面临诸多挑战。由于负载重量较大，堆垛机在运动过程中易产生振幅较大的机械振动，尤其是立柱振幅的增大，会直接影响设备的定位精度和运行效率。此外，重载设备的运行效率与振幅之间存在固有的矛盾：提高运行速度以提升效率往往会加剧振动，而降低振幅则可能导致作业时间增加。因此，如何在保证作业效率的同时有效控制立柱振幅，成为重载堆垛机速度优化中的关键问题。针对这一问题，本文提出了一种基于遗传算法的重载堆垛机速度优化方法，旨在保证作业效率的同时提高堆垛机稳定性。

二

超重载堆垛机立柱挠度

1．堆垛机力学模型建立

根据堆垛机的基本结构与质量分布建立直角坐标系：设堆垛机为满载状态，水平运行方向为Ｘ轴，且X轴通过两行走轮中心；载货平台起升方向为Ｙ轴，且Y轴通过左立柱质心。本文将堆垛机的运动简化为在XOY平面内运动，堆垛机结构简化如图1所示。

图1 堆垛机质量分布图

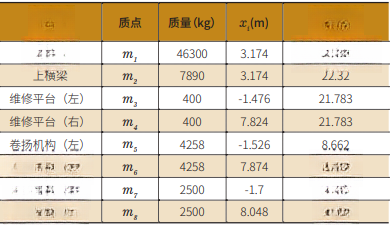
双立柱堆垛机为门架结构，当受到外载荷作用时，根据前人文献研究，左右立柱的挠度几乎一致[1]，因此，通常取其中一根立柱进行分析。本文取左立柱进行挠度分析，在分析其所受外部载荷时，仅考虑上横梁、维修平台、载货台及货物、卷扬机构、电控柜影响，质量分布情况参见表1。

表1 堆垛机各质点质量及坐标

2.叠加法计算立柱挠度

由于下横梁在堆垛机系统中相当于基座，因此不考虑其对立柱挠度的影响，即将下横梁视为刚体，立柱视为悬臂梁。堆垛机其他部分质量对立柱挠度的影响通过叠加法计算。

（1）各部分质量引起的挠度

堆垛机在运行时各个质点重量对立柱轴线产生力矩而导致立柱发生挠曲变形wM：

式中：h——立柱高度（m）；E——立柱的弹性模量（Pa）；I——立柱截面惯性矩（m4）。

（2）水平加速度引起的挠度

由于水平加速度各部分质量引起的惯性力导致立柱的挠曲变形wax：

式中：ax ——堆垛机水平加速度（m/s2）。

（3）垂直加速度引起的挠度

不仅各质点重力对立柱产生影响，而且在载货台加速垂直运动时，对立柱产生一个纵向压力，该部分产生的动态挠度为way：

式中：ay——载货台垂直加速度（m/s2）。

（4）立柱质量引起的挠度

立柱因自身质量产生的惯性力沿着立柱高度均匀分布，其产生的挠度wG：

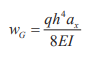
式中：q——立柱单位质量（kg/m）。

由于双立柱的结构，除立柱自身质量产生的挠度外，其余挠度均由两立柱共同承担，所以根据叠加法计算的单根立柱总挠度为：

将上式改写为与加速度相关的函数：

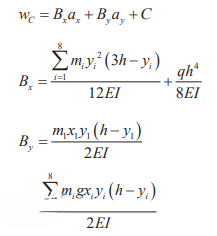
3.立柱挠度函数建立

由于本文所设计的超重载堆垛机起升质量较大，载货台位置对立柱挠度的影响不容忽视。基于立柱挠度分析，堆垛机运行过程中，挠度随载货台层高变化，Bx、By随之变动，故将其视为载货台位置y1的函数，其函数图像如图2所示。对于参数C，由于载货台由钢丝绳悬吊于上横梁，其与立柱接触的导轮在垂直方向上并不与载货台产生力的作用。因此，参数C不随载货台的升降而发生变化，数值为0.0058。

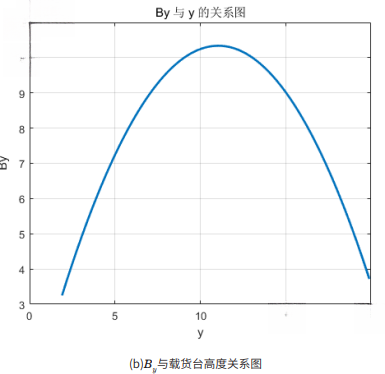
图2 立柱挠度参数与载货台位置关系函数图

图中显示，Bx、By变化幅度均较大，可证明载货台位置对立柱挠度具有显著影响。然而，若ax、ay的最大值均取值为0.3m/s2，Byay 项的最大值为3.18×10-8，其与Bxax项的最大值0.0126的比值2.52×10-6，与C的比值为5.48×10-6，由此可得Byay的值远小于Bxax与C的值。为了简化优化过程中的变量，降低计算复杂度，本文将忽略载货台加速度影响，专注于水平方向分析。

基于上述分析，将立柱挠度写为关于载货台位置及水平加速度的函数：

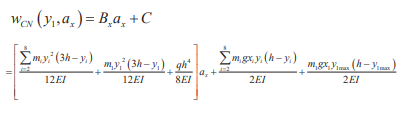
三

超重载堆垛机立柱振动方程

堆垛机作为自动化立体仓库系统中核心物料搬运设备，其运行稳定性直接影响仓储系统的整体性能。为确保设备运行平稳并有效抑制立柱过大振幅摆动现象，本节基于立柱动态挠度数学模型构建了其振动方程及Simulink仿真模型。

1.立柱振动方程数学模型

根据文献研究，可将堆垛机的摆动问题等效转化为理想状态下的单质点悬臂梁振动问题，其力学模型如图3所示。基于这一简化模型，可推导出悬臂梁的静变形曲线方程[2]。

图3 立柱简化图

由材料力学公式可知悬臂梁静变形曲线方程为：

式中：——自由端静力挠度（m）；m0—— 模型中单质点的等效质量（kg）。

假设悬臂梁做简谐运动，其动态挠度可表示为：

式中：——系统固有频率（rad/s）；A——振幅（m）；φ0——初始相位角（°）；t——时间（s）。

则立柱上各质点的位移方程为：

将以上位移方程对时间求导得到速度方程：

则悬臂梁的动能方程为：

可求出模型中单质点的等效质量。

根据自由端静力挠度可求得简谐运动频率为：

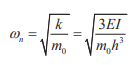
式中k=m0g/wm。

计算堆垛机立柱顶端的动态挠度，进而得到振幅为：

式中：vx——堆垛机水平运行速度（m/s）。

设初始相位角，则立柱顶端的振动方程为：

根据上式可知，对堆垛机平稳运行影响的主要因素是载货台高度y2、水平运行加速度ax及水平速度vx。并且振幅随载货台升高、加速度增大以及速度增大而增大。因此选择合适的速度曲线、协调水平和垂直作业顺序以及合理设置水平速度是有效降低振幅并且保证运行效率的关键。

2.振动方程仿真模型建立

基于振幅数学模型，采用Matlab中Simulink仿真模块建立堆垛机控制系统仿真图及其子系统图，如图4、图5所示。

图4 立柱振幅仿真模型

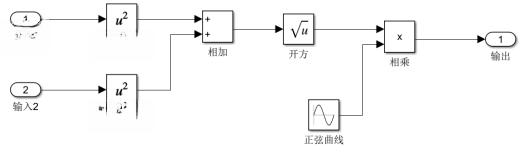
图5 子系统模型

在仿真系统中分别输入垂直速度函数，对其积分得到载货台的高度函数；输入水平速度函数，通过微分运算得到加速度函数，仿真图中系数1表示常数

四

不同速度控制曲线的数学模型

针对堆垛机在运行过程中高速、高精度、高效率的控制要求，其速度控制曲线应当保证堆垛机平稳运行，减少因刚性和柔性冲击而产生的振动，同时也应当保证加速、减速耗时短，快速达到指定速度或加速度。本节以前文建立的仿真模型为基础，分别采用抛物线型速度曲线控制方法与三角函数型速度曲线控制方法对堆垛机速度振幅进行仿真分析，对比在相同条件下采用２种运动控制方法的情况下堆垛机运动性能的变化，并选择最优速度曲线。

图6 抛物线型曲线速度、加速度、加加速度示意图

1.抛物线型速度曲线数学模型

图6为抛物线型曲线速度、加速度及加加速度曲线示意图。当堆垛机水平方向运行较长距离，整个加减速过程分为7段，t0-t1与t2-t3时间段为变加速阶段，t1-t2时间段为匀加速阶段，t3-t4时间段为匀速阶段，t4-t5与t6-t7时间段为变减速阶段，t5-t6时间段为匀减速阶段，其中Jm为加加速度最大值，am为加速度最大值，vm为速度最大值。

2.三角函数型S速度曲线数学模型

图7为抛物线型曲线速度、加速度及加加速度曲线示意图，整个加减速过程分为7段，和抛物线型速度模型的主要区别在加速和减速阶段，三角函数型加速度曲线消除了加速度突变现象，加速度过渡更加平滑。

图7 三角函数型曲线速度、加速度、加加速度示意图

3.速度控制曲线仿真及最优速度控制曲线

假设堆垛机满载，且载货台在运行过程中处于最高位置，两种曲线的最大加速度、最大加加速度、最大速度均相同。经Simulink仿真后，得到立柱顶端振动曲线如图8、9所示。

图8 抛物线型速度函数曲线振动仿真曲线

图9 三角函数型速度函数曲线振动仿真曲线

根据仿真分析图可知：在做变速运动时，三角函数曲线的振幅相对较小；两种速度曲线最大振幅基本相同，均为44.78mm，在堆垛机做较大速度的匀速运动时，最大振幅由最大速度决定。

但在相同时间内，抛物线型曲线运行距离为19.5m，三角函数型曲线运行距离为17.78m，在抛物线型函数运行效率更高，因此选择抛物线型曲线为最佳水平运行曲线。

五

基于遗传算法的运行效率与振幅协同优化

在上一节中，抛物线型速度曲线已被确定为超重载堆垛机水平运行的最优曲线。本节将进一步对该速度曲线进行优化，采用遗传算法（Genetic Algorithm, GA）对载货台垂直运动与堆垛机水平运动的协同优化问题进行研究。研究的核心目标是通过优化垂直与水平运动的协同参数，实现运行效率与立柱振幅的协调优化，从而提升堆垛机系统的整体性能。

1．条件假设

为了更清晰地表述问题并构建堆垛机路径规划的数学模型，本文作出以下假设：

假设1：堆垛机的位置信息及其所处环境信息均为已知，且系统的初始位置与目标位置由系统预先确定；

假设2：由于堆垛机的机械结构在水平方向上呈左右对称，因此水平方向的运动不区分左右方向。规定堆垛机水平方向至少移动一个货格的距离，当堆垛机运行较短距离，可能不存在匀速运动阶段，但必然出现匀加速阶段。规定水平方向的加加速度与最大加速度为固定值，但最大速度作为待优化参数，需通过优化算法确定。

假设3：基于前文的理论分析，垂直方向的运动速度与加速度对系统振幅的影响可忽略不计，因此垂直方向的运动可简化为匀加速运动与匀速运动的组合且加速度和最大速度为定值；

假设4：优化前的运动策略采用水平和垂直位移同时开始，且均以尽量快的速度到达指定位置的策略；优化过程中水平方向的运动和垂直方向的运动可以不同时开始，一个方向的运动开始后，另一个方向的运动在第一个运动结束之前的某一时刻开始。

2.模型及约束建立

相关设计参数及变量参见表2。

表2 模型参数及变量表

本文研究的问题是实现运行效率与立柱振幅的协调优化，因此适应度函数如下：

约束函数如下：

(1)水平速度约束

(2)运动顺序约束

若s=0，则垂直方向先运动，

若s=1，则水平方向先运动，

(3)运行时间约束

水平运动时间按照抛物线型速度曲线计算。

3.遗传算法过程

针对堆垛机水平与垂直协同作业的特点，设计了适用于动态作业场景的染色体编码方案、适应度函数及遗传算子。算法运行流程如图10所示，具体实现如下：基于载货台垂直升降与堆垛机水平行走的运动参数协同需求，构建染色体编码结构，使每条染色体能够表征不同作业阶段双轴运动参数的匹配关系。适应度函数依据堆垛机作业完成时间与立柱最大振幅进行设计，量化各染色体方案对协同作业目标的满足程度。在选择策略中，采用精英保留的分层选择方法，既保留优质个体又维持种群多样性；在交叉操作中，采用分段基因重组策略，通过动态调整交叉概率实现参数序列的优化组合；在变异操作中，采用自适应变异策略，随着迭代次数的增加，逐步降低变异概率，以平衡全局搜索和局部搜索的能力，避免过早收敛。通过迭代优化，最终生成堆垛机垂直－水平运动协同的最优参数配置方案，有效提升堆垛机作业效率及稳定性[3]。

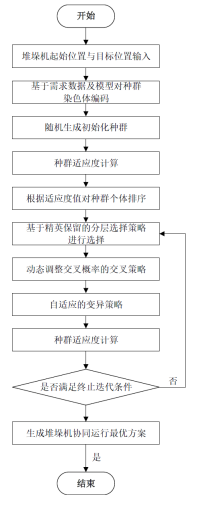
图10 遗传算法运行流程

4.优化结果及分析

为了验证遗传算法在堆垛机路径规划中的有效性，本文选取了四组不同的起始位置和目标位置坐标进行实验。每组实验的起始位置和目标位置参见表3。

表3 三角函数型曲线速度、加速度、加加速度示意图

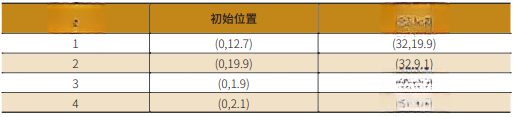
通过遗传算法优化，得到了每组实验的最优参数配置。图11表示实验组3的迭代过程，适应度值随迭代次数的增加逐渐收敛，表明算法能够有效搜索到最优解。图12表示实验组3优化前后水平速度曲线对比图。

图11 遗传算法迭代图（实验组3）

图12 实验组3水平速度曲线对比图

表4显示了全部作业的优化结果。通过遗传算法对超重载堆垛机运行效率与立柱振幅的协同优化研究，实验结果表明，该方法在降低立柱振幅方面具有显著效果。实验数据显示，优化后的立柱振幅降幅均超过10%，且作业时间未出现明显增加，表明遗传算法能够有效降低立柱振幅，从而提升堆垛机的运行稳定性。尽管长距离作业时间略有增加，但振幅的显著降低为系统的安全性和精度提供了重要保障。本文的研究为超重载堆垛机的性能优化提供了理论支持，为重载物流场景下的高效、精准作业提供了可行的解决方案。

表4 试验结果

六

结语

本章针对超重载堆垛机在运行过程中出现的立柱顶端振幅过大的问题，进行分析和优化研究。首先，通过建立堆垛机立柱的动态挠度方程，充分考虑载货台高度变化对立柱挠度的影响，并建立了立柱振动方程的Simulink仿真模型。接下来通过仿真对比了相同条件下两种典型的速度控制曲线的振幅和作业效率，并确定了抛物线型曲线为最优水平运行曲线。

为实现运行效率与立柱振幅的协调优化，本文采用了遗传算法对抛物线型速度曲线进行进一步优化。优化结果表明，遗传算法显著降低立柱振幅同时保证作业效率。

综上所述，本文的研究为超重载堆垛机的速度控制曲线优化提供了理论依据，有助于保证作业效率与提高堆垛机安全性。

参考文献:

[1]张恒.双立柱堆垛机结构静动态特性分析与结构优化[D].南昌大学,2024.DOI:10.27232/d.cnki.gnchu.2024.002400.

[2]张靖瑄.高速高加速堆垛机防摇摆分析及其智能算法的实现[D].机械科学研究总院,2020.DOI:10.27161/d.cnki.gshcs.2020.000029.

[3]冯润晖,董绍华.基于并行协同的多车间协同调度问题研究[J].机电工程,2023,40(01):122-128.

———— 物流技术与应用 ————

编辑、排版：王茜

本文内容源自

欢迎文末分享、点赞、在看！转载请联系后台。

广告宣传