继续预习

这节很简单，孩子学起来也不费劲，完全可以自己预习，但是：

记得，预习完，带孩子复盘一下。

复盘重点是一个学习方法——从多个角度理解一个知识点。

我们来看，课本首先还是化归。

还是化归

课本引入了一个例子：

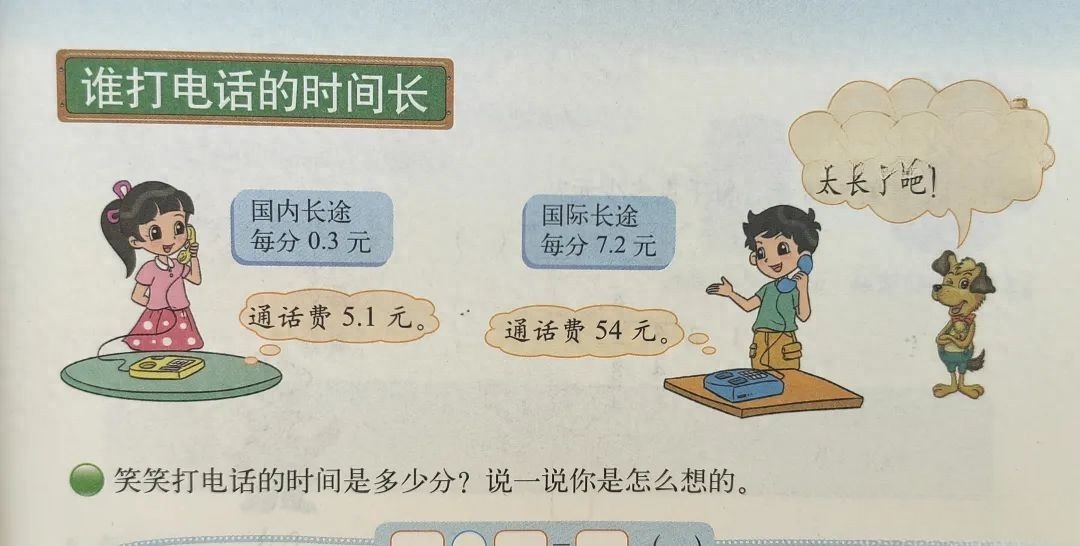
国内长途每分0.3元，通话费是5.1元，笑笑，打电话的时间是多少？

这道简单的应用题，列式可以是：5.1÷0.3。

可是，我们之前学的都是除数是整数的小数除法，现在除数不是整数了，该如何计算呢？

还是化归。

让不熟悉的小数除法，来到我们熟悉的领域——元换成角，这样就变成51角÷3角＝17（分钟）。

那还有没有别的方法呢？

我们上学期学过商不变的规律——被除数、除数同时扩大或者缩小同样的倍数，得数不变。

现在我们可以把5.1和0.3都扩大10倍。

扩大10倍后，便来到了熟悉的整数除法。

还不够

上面两种方式：

具体的元角分+商不变规律，已经帮助孩子理解了除数是小数的除法如何计算。

相信下次孩子遇到类似计算，完全可以自己得到结果。

但课本觉得还不够。

接着，用学小数时熟悉的方块图，让孩子圈一圈。

这一点有两层意思：

✔️5.1元，一分钟0.3元，我们可以看看5.1里有几个0.3，利用方块图圈一圈——在用除法的本质，告诉孩子们：结果跟被除数、除数同时扩大10倍的计算一致。

✔️0.3是3个0.1，5.1是是51个0.1，那么5.1里有几个0.3就相当于51里有几个3——进一步解释扩大10倍的方法为什么可行。

相对于具体的元角分，这是更抽象的解释，让孩子的理解更上一层楼。

之前我写过文章：除法的本质是【连续的减】，大家可以拓展阅读。

关于除法的方方面面，都在这里了：信息量太大，收藏了慢慢看

到这里，孩子们理解了：同时扩大10倍来到整数范畴，计算会很方便。

那我们把这种计算方式固定下来，好不好？当然好。

于是，淘气示范了竖式的操作方式：

去掉小数点，被除数、除数同时扩大10倍；

按照整数除法的方式来计算，得出的答案就是我们想要的。

验算一下，也没问题。

多途径、多方式

你看，课本并没有直接告诉孩子们：我们扩大10倍来计算。

而是带孩子探索、理解为什么要这样算，且用了多种方式：

✔️具体的元角分；

✔️商不变的规律；

✔️形象的方块图；

✔️抽象的包含除。

方方方面，帮孩子理解。

我们在帮助孩子学习、孩子自己学习时也要耐心：

一种方法说不通，就用用别的方式；

一种方式能理解，不要停止，再找一种方式。

用多种途径学习一个知识点，能够调动更多的神经元。

那么，将来涉及到这个知识点，很多神经元会一起联动：

如果是做题，这就意味着快速和正确；

如果是创作，这就意味着创意和活跃。

记住这种学习方法。

探索

接着来到试一试环节，鼓励孩子自己探索。

被除数，除数同时扩大，扩大到什么程度？

有了前面的积淀，相信孩子可以明白：

扩大到除数是整数就可以了。

这一点还是让孩子讲一讲，说一说——能说出来，记忆加深，也说明真懂了。

说完就到了练习部分。

试一试的练习要做，刚探索完巩固一下嘛。

再做课后的第2题和第5题。

第2题让孩子再巩固一下之前的理解；

第5题针对本节学的计算方法，练练手。

到这儿总结一下：

这节内容不难，孩子完全可以自己预习；

但通过这节可以给孩子讲一讲学习方法；

最后别忘了让孩子讲一讲，讲出来我们才知道孩子理解没，孩子也能通过讲解加深印象。