这是一次实战案例分享，里面藏着真知灼见。

前几天我在整理中考题，偶然让藤藤来做一道。本以为他一分钟就能做出来，结果花了四五十分钟，不只是做题，是连做题带讲题带总结。时间花了很多，但很值得。

这是南京市2024年中考数学最后一道填空题，其实考察的是基本定义。

一个根是x=2，这个显而易见。关键是第二个根，怎么求？

首先需要说明的是：一元二次方程求根的知识要到九年级才能学到，藤藤现在只是七年级，按道理是不会的。但是由于之前两个假期他通过自主预习，初中数学所有知识已经大概过了一遍，所以具备解决这种问题的基础。现在做这类题，能不能做出来不重要，重要的是查漏补缺，以练促学。

果然，他在解决第二问的时候，遇到了巨大的困难。其实困难的本质很简单，就是他对于这部分知识的印象模糊了。比如，他记错了求根公式。

如果求根公式记错了，我们是不是可以尝试自己从头推导一遍？

在他艰难推导的过程中，我发现卡柱他的很多细节。注意，细节非常重要。

ax²+bx+c=0。

第一次：他把c挪到方程右边ax²+bx=-c，然后两边同时除以ax，变为x+b/a=-c/ax。他这么尝试的目的是左边直接找到x，但右边还有x，就推不下去了。

第二次：他尝试把ax²直接拆成(√ax)²，c是(√c)²，也不行。

他胡乱尝试了几次之后，我不得不打住了。但是没有告诉他正确的方法，而是让他自己写了一个最简单的一元二次方程，自己试着凑平方。

他写了x²+4x+3。这时候他知道是x²+4x+3+1-1=(x+2)²-1。

我让他对照着自己写的模板，再思考。

第三次：他先写了一个ax²+bx+c+1-1，给我看乐了，这显然是照搬照抄。

第四次：他想到了需要2，所以先把方程改为2ax²+2bx+2c=0，然后又打算用(√2ax)²，(√2c)²来凑平方。

这个过程很纠结，我也克制了直接告诉他答案的冲动。也是看着时间耗费太长了，又给他一个提醒，就是给他一个样例：3a²+4a-3=0

这一回，他居然一气呵成：

3(a²+4/3 a-1)=0

a²+4/3 a-1=0

a²+2×2/3×a-1=0

a²+2×2/3×a+(2/3)²-(2/3)²-1=0

(a+2/3)²=(2/3)²+1=13/9

我发现他完全会凑平方，于是让他对照这个过程，再来一遍。这一回，他快速理解了问题的卡点。

ax²+bx+c=0

a(x²+b/a x+c/a)=0

x²+b/a x+c/a=0（我说你没发现自己多了一步吗？提取a那一步是多余的）

X²+2×b/2a×X+c/a=0

X²+2×b/2a×X+(b/2a)²-(b/2a)²+c/a=0

(X+b/2a)²=(b/2a)²-c/a

(X+b/2a)²=(b²-4ac)/4a²

X+b/2a=±√(b²-4ac)/2a

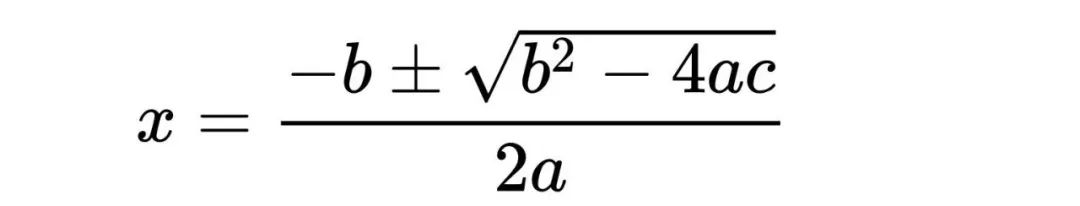
我跟藤藤说：你这一遍推导得非常完整，你总结一下每一步的关键。下面是他的总结。

第一，把二次项系数变为1；

第二，一次项系数前面提出一个2；

第三，除了2以外的一次项系数进行平方，加上一个减去一个……

其实，他之前听这部分课程的时候，一定听过讲解，老师讲解的可能比这个更准确更清晰。但老师怎么讲是一回事，你有没有听进去是另一回事。你有没有同步推导？你有没有暂停思考？你有没有用自己的语言完整地解释一遍这个过程？

很显然，藤藤之前并没有做到。但也因为只是自主预习，所以我也并没有要求他做到这个程度。只是通过今天这个练习，倒逼他思考应该怎样听课怎样学习。

解决这道题的细节还有很多，这里就不啰嗦了，有一个关键问题引起我的思考。

你会发现，我没有直接告诉藤藤答案，而是让他自己写了两个简单的例子，自己照着例子对比分析，最终也找到了解决方案。第一个例子是最基础的结构，让他认识到一次项系数前面的2；第二个例子是基础的变形，二次项前面有系数怎么办？他自己知道要先变为1。

为什么他看到数字3，马上就知道消掉，但见到a就不知道消掉呢？这就是数学学习的一个关键难点：只要一个符号的变换，就可能造成巨大的认知瓶颈。字母a是系数，是相当于数字3的常数，但这个常数又是不确定的，恐怕藤藤当时的头脑中对于这一点还没有深入理解，所以会遭遇到巨大的认知困难。

通过这个例子我想说明什么？

第一，学习数学必须循序渐进。你要先学会x²+4x+3如何凑平方，然后再学3x²+4x+3如何凑平方，最后再来理解ax²+bx+c如何凑平方。每一次只改变一个关键条件，每一次只往前走一步，你才有可能步步做到。绝大多数数学困难，是因为你跳步了。

第二，学习数学必须字斟句酌。3和a，仅仅一个字母之差，就会造成认知障碍。你必须真正理解每一个字母的含义，不要急于求成。每一个字母和符号都搞懂了，整个问题也就自然懂了。相反，很多学生懒得下这种笨功夫，所以数学始终一团糟。比如我问很多高中生，什么是“奇变偶不变，符号看象限”？能够完整准确说清楚的学生并不多。

第三，学习的过程犯错是必然的。学习的本质是从不会到会的过程。犯错是必然的，不会是必然的。今天举的这个例子其实非常简单。但简单是相对于学会的同学说的，如果你刚开始接触，有很多地方卡住了非常正常，没有必要大呼小叫，甚至冷嘲热讽。即便我辅导藤藤的时候，也经常要克制自己说教的冲动，有的时候态度也不太好。所以我常说，孩子学习的过程，其实更是对家长的考验。家长没有成长型心态，很难培养成长型心态的孩子。

智慧的父母，能够帮助孩子正确面对问题，摆正心态，不急不躁。一遍不行就两遍，两遍不行三四遍。在真正学会之前，多少努力和时间都是值得的。

我可以用一分钟让藤藤学会这道题，但那是我的知识，不是他的。他的尝试、犯错、思考，都是值得的。

我们花了更多的时间，学会的不是这一道题，而是解决问题的思路和方法，是学习行为的细节和重点。他有总结，我有收获，而且最终也能其乐融融，这一点尤其难得。

学好数学不容易，挑战虽然多，但只要心态好、方法好、习惯好，就能一往无前，赢得胜利。