通过对2025年福建九地市质检卷"综合与实践"题目横向对比分析，现总结以下重要规律和特征，并提出备考建议，供同行参考。

一、命题内容的三级分类体系

1.几何操作型（占比55.6%）

龙岩"23题：矩形分割成无盖纸盒表面"

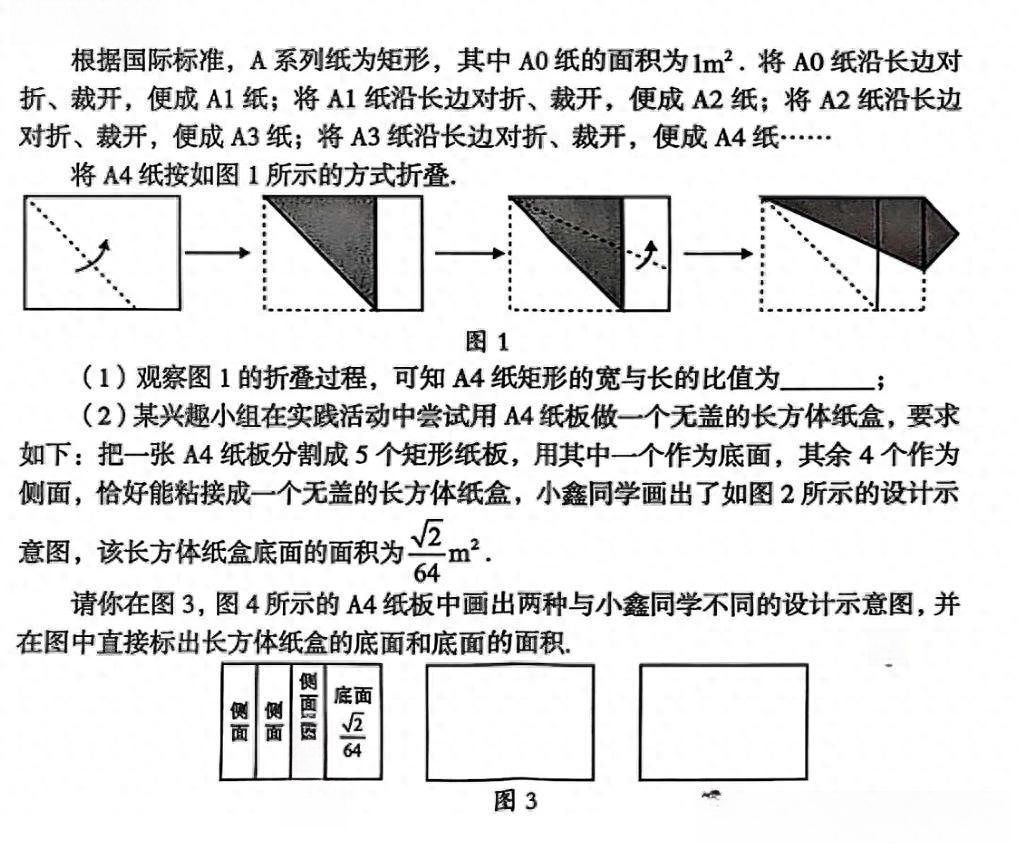
2025龙岩质检题

福州"24题：矩形切割成八边形"

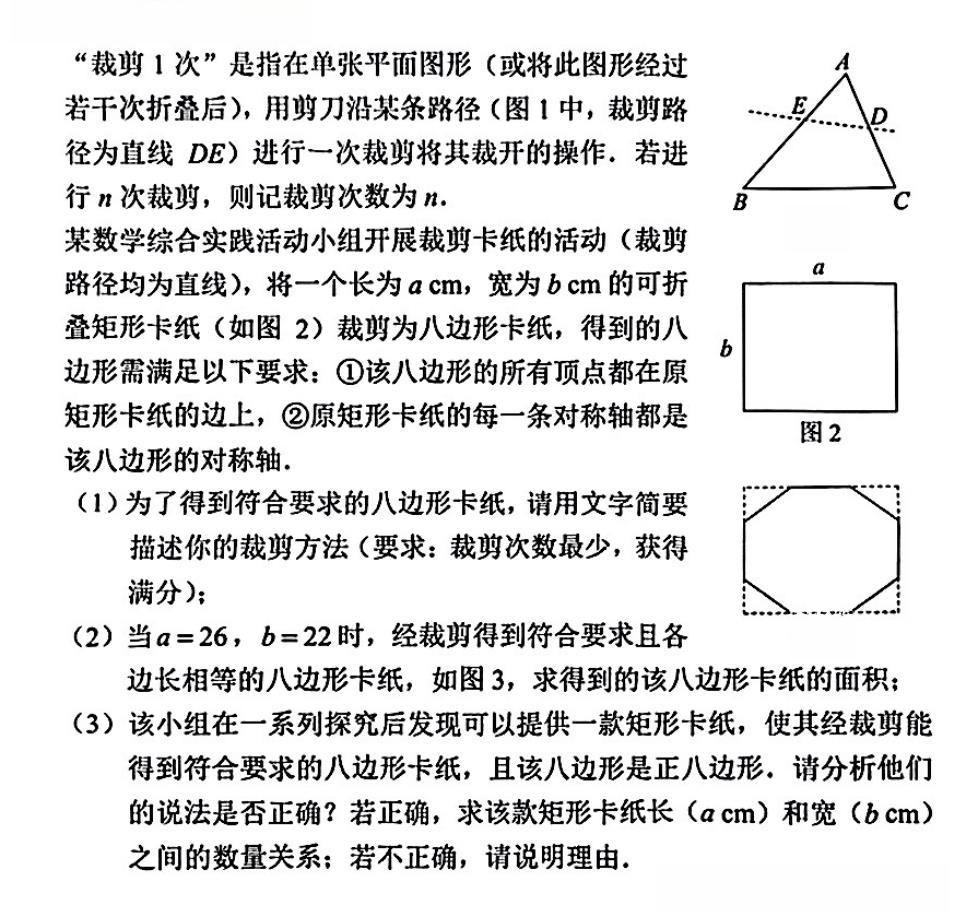
2025福州质检题

厦门"23题：矩形分割成正方形"

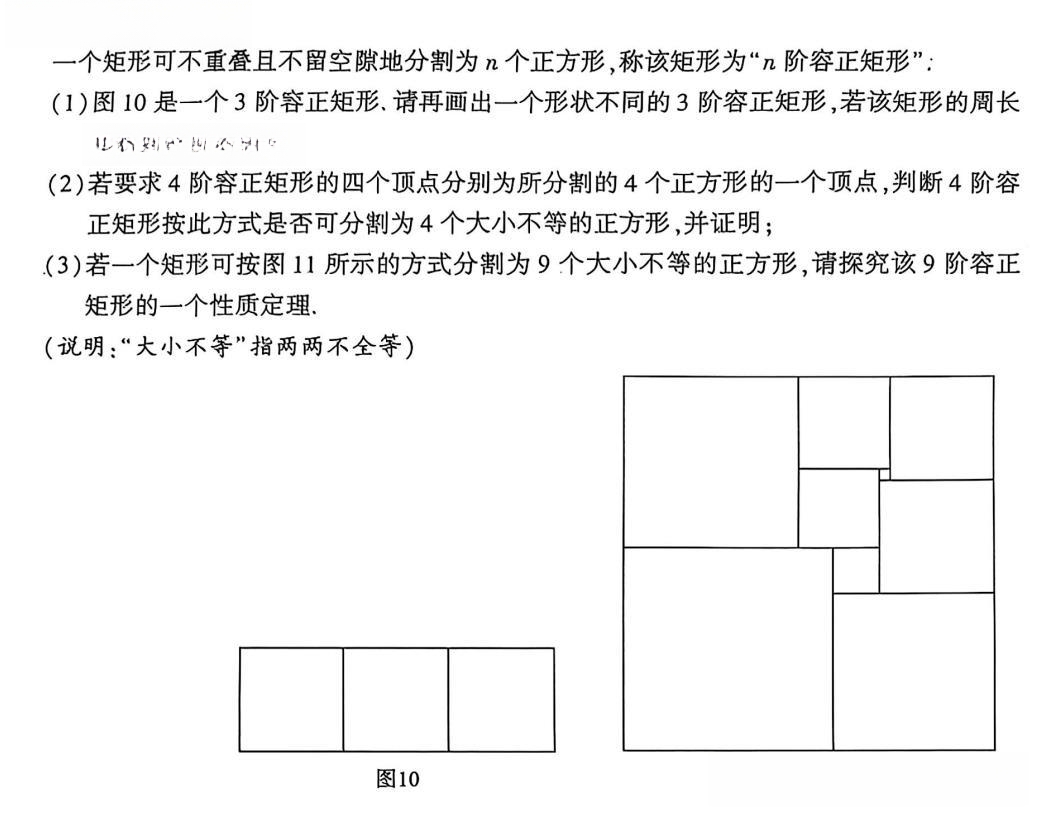
2025厦门质检题

莆田"23题：尺规作两倍面积平行四边形"

2025莆田质检题

宁德"24题：弓形的面积与估算"

2025宁德质检题

核心特征总结：均以几何图形变换为实践载体，强调动手操作与空间想象

1.数学建模型（占比33.3%）

漳州"22题：用三角函数测量"

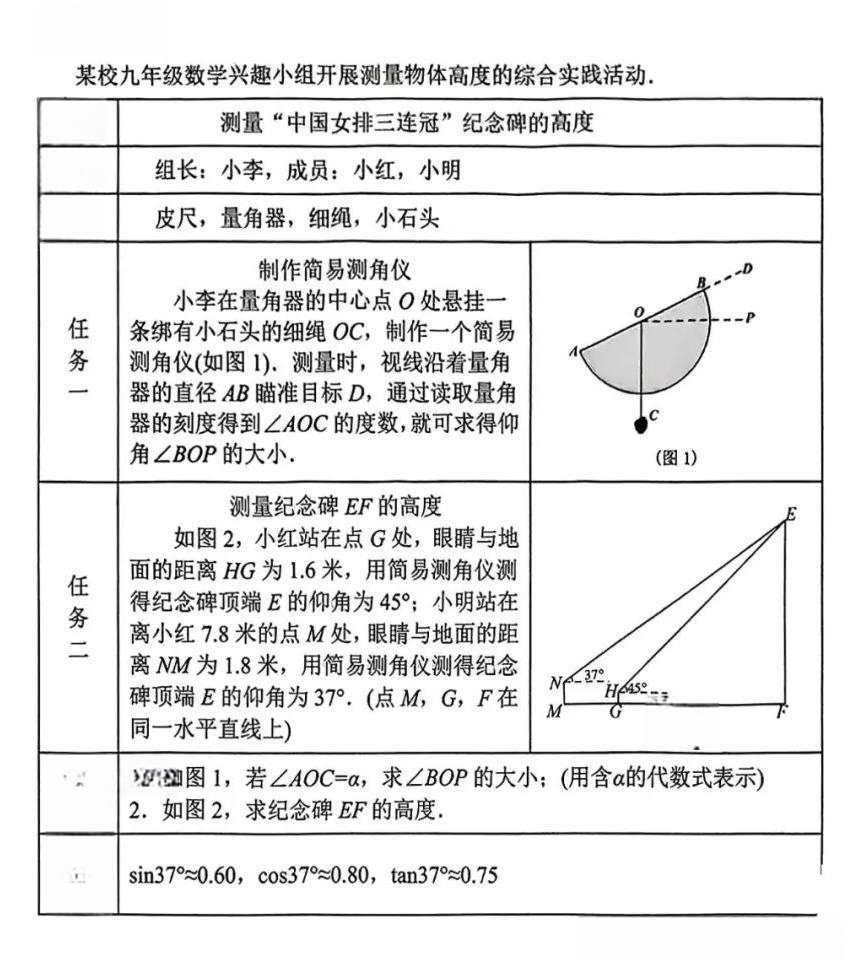
2025漳州质检题

泉州"24题：长方体的摆放"

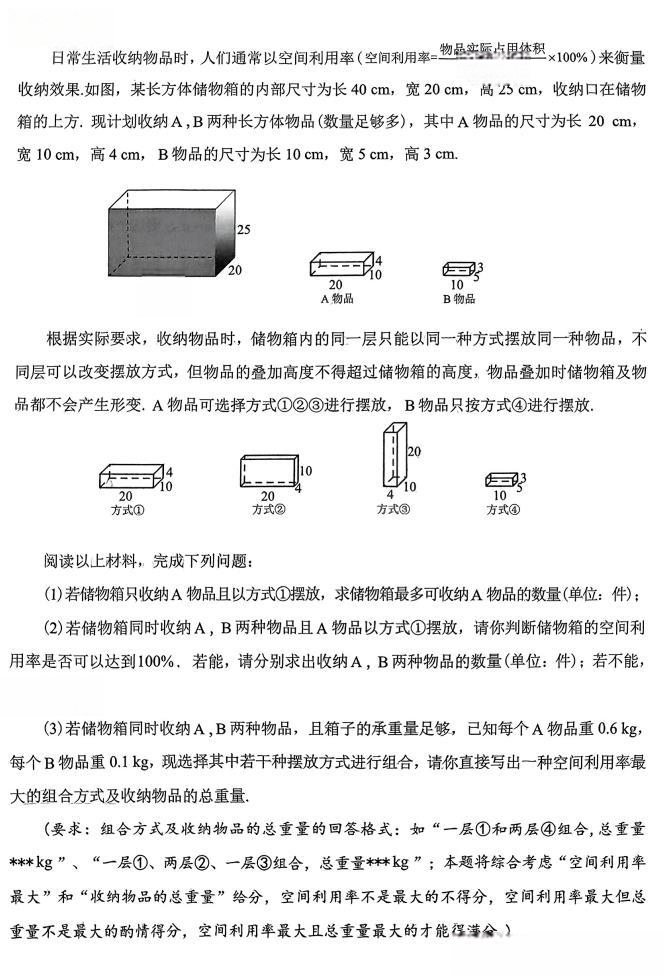
2025泉州质检题

南平"24题：函数应用（解决问题）"

2025南平质检题

创新点总结：将数学工具应用于实际场景，突出建模思想

3.代数应用型（占比11.1%）

三明"23题：一次方程+分类讨论"

2025三明质检题

特殊价值：唯一以代数方法为核心的实践题型

二、地区特色发展轴线

1.几何变换主线

龙岩-福州-厦门形成"矩形分割"系列：

龙岩侧重立体展开（无盖纸盒）

福州挑战复杂多边形（八边形）

厦门研究基本图形（正方形）

莆田独辟"尺规作图+图形缩放"路径

宁德专注曲线图形（弓形）

2.应用建模主线

漳州"三角函数测量"体现工具性

南平"函数应用"突出模型构建

泉州"长方体摆放"融合空间规划

3.三明代数单点突破

唯一采用方程解决实际问题

引入分类讨论思想

显示代数方法的实践价值

三、关键命题规律

1.题号定位规律

基础应用集中在23题：题（龙岩/厦门/莆田/三明）

综合实践延至24题：题（福州/泉州/南平/宁德）

唯一22题：题（漳州）体现考查前置

2.能力考查维度

几何直观（龙岩纸盒展开）

空间推理（福州八边形切割）

模型思维（南平函数应用）

估算能力（宁德弓形面积）

3.重要启示

莆田"尺规作两倍平行四边形"：唯一考查图形缩放

三明"一次方程+分类讨论"：唯一代数实践题型

这两类特殊题型可能成为创新风向标

四、2025年备考建议

1.几何操作训练

掌握基本图形分割方法（研究厦门、福州题）

训练立体展开图还原（对接龙岩题型）

突破复杂图形构造（学习莆田缩放思想）

2.应用建模准备

三角函数实际测量（参考漳州题）

函数模型构建（分析南平题）

空间规划问题（研究泉州题）

3.代数应用突破

方程实际问题建模（借鉴三明题）

分类讨论策略（掌握三明题方法）

五、2025年命题预测

1.几何操作题可能向"组合图形+参数设计"方向发展

2.应用建模题或增加跨学科元素（如物理测量）

3.关注代数实践题型（跟进三明模式）

特别关注漳州将综合实践题前置至22题的设计，这可能反映对实践能力考查的强化。同时，莆田尺规作图与图形缩放的综合考查，以及三明代数方法的创新应用，都值得在备考中重点研究。建议建立"几何-代数"训练体系，既要巩固主流几何实践题型，又要对新兴代数应用方向保持敏感。

如需深入了解题目相关原卷和解答，请到个人主页搜索文章，欢迎评论区讨论。