Cogito ergo sum.

----Renatus Cartesius

据说，笛卡尔曾在一个晚上做了三个奇特的梦。第一个梦是，他被风暴吹到一个风力吹不到的地方；第二个梦是他得到了打开自然宝库的钥匙；第三个梦是他开辟了通向真正知识的道路。这三个奇特的梦增强了他创立新学说的信心。这一天是笛卡尔思想上的一个转折点，也有些学者把这一天定为解析几何的诞生日。

从笛卡尔写下《几何学》并创立解析几何开始，后世数百年，这种大一统的梦想一直在指引着人们。黎曼在1954年的讲师试讲中发表了《论几何学之基础假设》奠下了黎曼几何的基础，他考虑真实空间的维度以及该用什么几何来描述。克莱因在1872年发表《关于近代几何研究的比较考察》认为几何的目的是研究群变换下的不变量，后世称之为爱尔兰根纲领。不止是数学，二十世纪的巨浪更是在数学和物理的峡湾间激荡。广义相对论、诺特定理、杨米尔斯理论、标准模型理论……喷涌而出。

陈省身指出，这种密切的关系是“同气连枝，同胞共哺”，并给出了如下的图像：

不过，要知道所有的这一切，都开始于简单的笛卡尔坐标系。

亲爱的小朋友和大朋友们，你们早在上学之前，就明白很多事了。不会算面积并不妨碍牙牙学语的你们挑选最大的那块蛋糕；你们也知道往左爬可以再爬回来，但撒掉的果汁则一去不复返。

上学后，知识充盈着你们智慧的脑瓜。你们知道两个相同的三角形可以拼成一个平行四边形，也能割成一个矩形，然后你就会算面积了。不过你们想过没有，为什么长乘宽等于宽乘长？你们也知道所有和圆有关的题目都有圆周率π。那是否疑惑这个总也写不完的数字是怎么来的。为什么角边角和边角边都能决定一个三角形？回字有四样写法，但是勾股定理有几百种证法，你知道么？于是店内外洋溢着快乐的气氛。

在往后的很长时间里，你们的老师会告诉你们，这就是数形结合。同一个问题可以用代数来算，也可以用几何来看。等你们上了大学，有些幸运的宝贝会开始学一些真正的数学。书里会告诉他们，因为有些问题是同构的，甚至同构有哪些性质，所以我们才能这么做。

不过，在我看来，更重要而基本的问题是，同构带来了什么？同构来自于什么？即同构能否被拆解为一些更基本的性质？

虽然完整的推理过程是从具体到抽象的，但作为一个教员，现在请允许我倒转故事的讲述顺序，从抽象到具体的告诉你们这一切是怎么回事。

1、我们的世界

我们所在的世界性质良好。之所以我们可以数形结合，是因为在这个世界里，几何构型被造就成了满足某些代数规律的样子，就是说他们同构了。这样你操作一样东西的效果，和操作另一个差不多一模一样，就像照镜子一样。

注：请允许我简化一下问题，数学大的分支有代数、分析、几何等，小的分支更是不可胜数。代数在初等和高等数学中也各有不同的含义。这篇小文中不妨将所有非几何的都称为代数，问题不大，情绪稳定。

先回答第一个问题：同构带来了什么？它能帮助我们计算，我们已经知道这点了。这个答案可不够好。

更惊人的答案是：在一个宇宙中内嵌了对一套代数结构的同构，就可以无成本的计算。当你画出直角三角形两条垂直的边，就能量出斜边长度的时候，就该知道我在说什么了。

或者我也可以说：几何就是一套查找表。当然视域稍微扩大一点，可以把几何看成一种转换函数，有了它就可以在某个世界中降低存储和计算成本。这么说来，几何其实只是某种有帮助的幻象，它满足了某些代数结构，因而给我们以直观。

我们无论是用算盘、经典半导体计算机，还是用生物计算机、量子计算机，都是在用物理规律背后的代数结构来计算。这种用一个计算系统代替另一个计算系统的操作，是加快计算速度的不二法门。

于是，我们也完全搞明白了，科学研究在做什么：我们要找到这个宇宙内嵌的O(1)查找表、以及其他不同复杂度的函数都有哪些。找到这些代数结构的过程，也是不断接近终极理解我们世界的过程。

2、可能的世界

我们所在的世界性质良好。不是最好，也不怎么差。

从宇宙的宇宙（无数个可能宇宙）级别考虑，其他的宇宙完全可能有不同的几何，即有不同的内嵌代数结构。没有广义相对论和量子论的宇宙，或说只有牛顿平直宇宙对应的几何结构，也未必不能存在。反过来，加入更多限制的宇宙说不定也有可能。

当然，不同宇宙的不同限制下，如果基础的代数结构变了，有两个需要注意的事：

①、代数结构的不同组成部分之间以及其高层推理的结果要自洽，不能产生矛盾；

注：量子引力就让人有点头痛；不满足排中律的拓扑斯也是如此。我们后面也会看到三元数不存在，而四元数丢失了一些性质。

②、不同代数结构之上可能的演化也完全不一样。

注：说演化，已经戴上了有色眼镜。实际上一个宇宙可以不含时间（静止的宇宙并不产生矛盾），也完全可以把时间和其他维度等同对待，然后把历史上所有的时刻打包在一起，作为整体看成一坨。不过，从刻板印象来看，有时间的宇宙，如果加载的代数结构太奇葩，就有所谓解的存在性和光滑性问题，一不留神就化作烟花飞散了。自然也不会有智能生物去思考它的存在。

总之，和我们的世界一样，只要有一个内嵌了某些代数结构的几何世界，在那里同样也可以数形结合，也可以简化某些计算。

下一个问题是，这些不同的宇宙之间有什么关系？可能存在满足一个宇宙，但不满足另一个宇宙的部分代数性质吗？如果可以，就说明代数结构按相容性是可分的。有更多限制的宇宙，可以看成更少限制宇宙的子代宇宙。肯定有的吧，哥德尔不完备定理就说了点这事。

我们甚至还能在有不同内嵌代数结构的宇宙之间，根据它们能否完全或近似的互相模拟来评估它们的接近程度，即通过这两个宇宙的计算系统是否可互相替代来度量。

比如在我们的世界，可以用其他代数结构来计算指数，但这个过程需要额外花费时间。从时间切片的视角，我们这个宇宙对指数无能为力。这不妨碍存在另一个宇宙能很幸运的做到这一点。

也有的宇宙可能不存在满足勾股定理，因而可以直接量出直角三角形斜边的代数结构。所以我说，此处的宇宙，不是最好，也不怎么差。

再补充几点：

①、我们现在可以把几何世界认为是必须更严格自洽的世界，因为它需要某种某时切实的存在，而代数世界可以更天马行空一些；

②、既然可以用代数结构来作为几何世界的底层，反过来几何可以作为代数的底层吗？也不是不行，不过对这位造物主的虚拟机要求可能就更高一些，限制也更多了；

③、有没有几何能表示，但代数不能的世界？现在看起来不太可能。

3、勿在浮沙筑高台

前面两章，我们回答了第一个问题，同构带来了什么。现在该到第二个问题了，同构来自于什么？

数学中第一重要的概念是相等。

紧接着相等，我们可以产生一系列概念：

①、有相等就有不相等，这产生了大小或序关系；

②、进而可能有多个成分，于是就有了维度；

③、维度多了便有了函数，也有了物理世界中的量纲和守恒等；

④、信息太多了，丢掉一些，得到了不等式和概率等；

⑤、当然上面所有的一切都可以有连续和离散。

3.1、相等

即便是进化的本能，也要求我们能判断哪些是相等（一类）的。我们要能分清敌友、哪些能吃、哪些要躲、哪些值得爱。

对相等关系的进一步扩展，产生了群，以及对称性。这深入下去就有了抽象代数领域中的一大类研究。

同一个代数结论可能映射到好几个几何过程。比如我们说过勾股定理的几何证明已经有了几百个，我们还将知道圆周率π，可以有不同的展开式。为什么会有这种一对多的映射？是否这些不同的几何过程之间也有对称性？它们是否来自于代数的对称性？如果想深入研究，小朋友们可以了解一下子群的概念。或者对女生宿舍四个人五个群的都市传说莞尔一笑。

3.2、序

如果有两个不相等之物，我们还能对其下什么结论吗？好、坏，好人、坏人，好吃、不好吃，好玩、不好玩……

偏序关系是对不相等的方向性扩展。而且还可以进一步分解一下：能往一个方向走，再回来的，是双向；只能往一个方向走，但回不来的，是单向。好了，亲爱的读者，你现在知道空间和时间，无非也只是一个是双向、一个是单向而已；一个是直线、一个是射线而已；一个无因果、一个有因果而已。

等等，那边有个小姑娘提问：为什么离开了相同的不同，只有两个方向，难道不可能有多个方向吗？

好家伙，上道啊。这不是完全没有可能，但是如果有多个方向，我们为着简化考虑，不妨将这些不同的方向分开，于是我们有了：维度。

3.3、维度

维度，可以看做是能用于比较大小的特征。有多个特征于是就有了多个维度。More is different。

其实，到此为止我们已经构建出了代数世界和其几何映射的大部分基石。我们完全可以认为：平面或更高维空间是想象出来的，实际上只有坐标的组合。这种视角，完全不会产生任何矛盾。

数形结合就是不同维度的组合，内蕴了某种代数结构。而我们可以直接观察到这个结构而已。这里的观察，用查找一个查找表来代替，毫不违和。

等等，这次是个小猴子在问：坐标有了，查找表在哪？

多的很，小朋友你要哪一本？

3.4、函数

函，盒子也。函数是一个黑盒子，它可大可小，什么都能往里放，也什么都可往外拿。你可以garbadge in garbage out，也可以大变活人。放进去什么，又拿出来什么，全凭你（魔术师）的心情。

函数就是为了处理多个输入的坐标，通过内部一通乱算，得到查找表的过程。当然，这个过程要自洽，相同的输入搞出不同的输出，这盒子就是个坏盒子。这个一通乱算，管你里面怎么算的，我现在而今眼目下，马上就要。这就是魔术师的底气。

最简单的函数是加法。输入两个数得到一个数，诚不我欺。减法，不仅是函数，也可以看作加法的一种。

假设a和b都是正数，而b又大一些，推广上面这个操作，从两个数得到一个数的函数，结果似乎肯定在[b-a,b+a]区间内。于是，这个函数的两个极端情况就是减法和加法。新函数的结果，可以看成一个双截棍。当短的那节绕它们共同的连接点旋转时，整条双截棍在长节所在边上的投影长度，正是我们新函数的输出。

我们刚才是把短边在长边投影，我们当然还可以让长边在短边投影。我们甚至可以要求对称性：无论以哪一条边作为主要边，函数的输出必须相同，有没有可能？当然了，这时我们有勾股定理，输入两个直角边，得到斜边长，也是个函数。

不同的维度之间，可以正交，也可以有相互关系。正交，即一个维度上移动了一下，完全不会影响另一个维度上的数值。这种变化也可以由函数体现出来。作为勾股定理的扩展，有边角边得到对面斜边长的余弦定理。

我们还可以更广泛的定义距离。前面不是说过，直角三角形量一下斜边即可？别急，那只是其中一个函数而已。

我们可以随自己心情，搞出一堆新的距离：

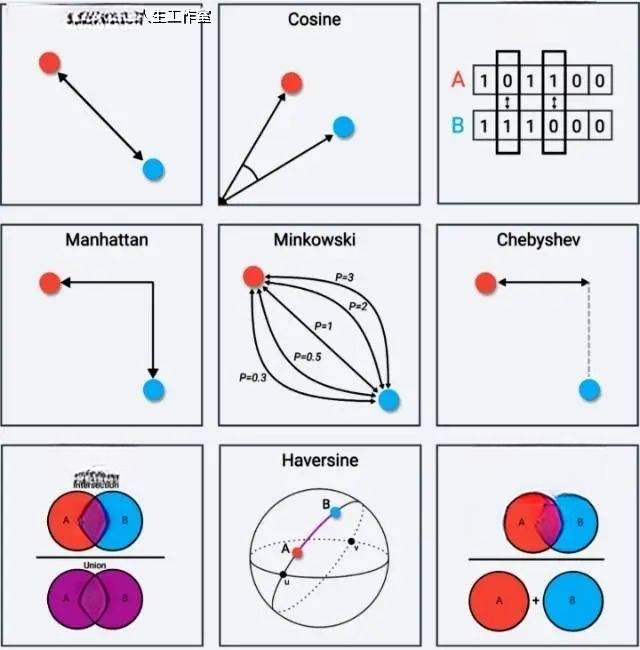
注意，一行一列就是所谓的欧式距离，它是最常用的，也是学校里教过的那个。而二行一列是曼哈顿距离。当你在垂直的街区中穿行，而不能凌空飞过楼房就该明白我在说什么。其他距离，留作课后作业，下课。

等等，不会都走了吧……

在几何的世界中，可以有距离、面积、周长、体积……但现在开始你要知道，它们其实都是不同函数的不同马甲而已啊。小样，别以为你穿上马甲我就不认识你了。

当然，一个几何世界可以同时加上很多函数，除了前面说过的，函数内要自洽，一个输入不能搞出不同的输出。不同函数之间也要自洽，函数的组合也要自洽。你如果先迈左脚再迈右脚会走到冰淇淋店，先迈右脚后迈左脚却会掉进火山岩洞，想想就刺激。

注：奇怪的世界总是有的嘛，非交换代数，以后再安排。如果大朋友学过线性代数，也知道矩阵乘一般是不可交换的。这里就别吓着小朋友了。

一般来说，我们觉得不同的维度应该有等效性，或者说维度间的对称性。于是要求函数的某些输入之间互换不影响结果，而另一些维度之间不可互换。即维度是分组等效的。

一些函数的参数可交换性体现在：距离、引力、电磁力等上。所谓力的作用是相互的，就植根于空间维度的对称性上。而空间和时间维度一般不可互换。其他一些对称性，比如托马斯回旋性（某个未来才会被发现的对称性），你很好奇，但我只会敲你的头三下。

平面是最简单的让两个维度发生关系的地方。但两个维度不必然需要发生关系，发生关系的函数也可以有很多种。

当我们为多维空间加上了各种枷锁：加法封闭、乘法封闭、距离、范数、内积、完备化……它就会成为具备良好性质的空间。或者说，加载了特定函数的空间。

可以再补充几句：

①、所有函数都可以几何化，或者你能在想象中把它几何化，只要有没有成本的查找表就行。比如三体问题就是有三个实体，又都符合引力方程之后的交互行为。你也完全可以想象，二维或高维世界可能的引力是怎样的；

②、我们也可以通过有限来研究无限（下文有无穷级数展开）；

③、有多元函数，当然也有多元群。

3.5、量纲

如果说几何是代数的特例，那物理又是几何的特例了啦。

量纲是物理量的基本属性，有长度、时间、质量等等。又分为强度量和广延量等，前者随空间扩展会改变，如质量、能量，后者则不随空间延拓改变，比如温度、压力等。

物理公式也是函数啊，可以看作不同维度的参数经过特定函数得到结果的过程。或者这么说，同一个世界中内嵌了好几个互相可以匹配（一起算）的维度。当然，有些维度能一起算，有些维度不必然能一起算，即对应的函数不存在。你要是把面积和力相加，数学和物理老师都会气疯的。

量纲的存在为一个函数添加了更多的参数间限制。这种种（包括下节守恒量的）限制，除了让我们虚弱，没法徒手引爆小宇宙，也稍微带来了一些工程上的好处。有所谓量纲分析。比如英国力学家泰勒，仅根据1947年公布的原子弹照片序列就估计出了其爆炸当量。

不得不提的一句是，物理中随着问题的复杂，维度不断增加，一个个写参数太麻烦了，于是有了向量。向量的维度需要继续提升，就变成了张量（麻辣烫bushi）。

对于这些参数间限制，有些我们还找不到原因的，就会给它们一个名字，叫作物理常数。要知道标准模型中就有一堆可调参数。如果你觉得调热水器的冷热是在火山和冰浴之间抉择，想想更多的旋钮吧。

3.6、守恒

好像觉得限制还不够多一样。我们还有一堆守恒量：能量守恒、角动量守恒、动量守恒、电荷守恒……

这其实是有好处的，如果没有这些限制，函数的输出再传给函数，就可能指数增长，然后砰的一声，所有一切都化作了漫天花雨。当然，不劳而获这种事也是不用想了，世界不会凭空多出些什么东西。这样的宇宙，也才有可能发展出文明，记录下这一切（人择原理）。

在此，让我们致敬诺特和她的诺特定理，展示了守恒量和对称性之间的神秘关系。

全局的守恒当然是重要的，但局部的不守恒却是被期待的。难道我们不能像有个银行一样，临时的借一点钱再还回去吗？

波尔在中微子没有发现之前，就短暂的怀疑过能量守恒。费曼图中的虚粒子也可以看做一个偶然可以操纵的账户。

而一个虽然变动不居、忽大忽小但整体稳定的小世界，也作为全局的一个局部而经常出现，比如生活在布朗运动或股票涨跌这样小世界中的小人，就会得出和我们不一样的结论，我前面也提到过拓扑斯。

物理中还有一些著名的限制，如最小作用量原理、洛伦兹变换、度规张量等等。怎么你还要说？

3.7、不等式和概率

面多加水，水多加面，这可什么时候是个头啊。就像另一个教员说的：把炮沉掉。必要的时候可以丢掉点信息了。

如果我们因着某个对重要性的判断，丢掉某个维度的一部分不重要数据，我们就获得了不等式。此时我们只关心某维度中的一段区间，而这个区间就有了概率。故而，不等式就是统计之始。

想想看，布丰投针实验，是不是把不等式和概率联系了起来。

我们还可以压缩掉整个维度！

博弈论是什么？你不妨把它看成未来所有的时间维度都压缩掉了。你只能做当前的一步操作，但是要选择一个未来可能的最好世界。由量子效应主导的物态，用拓扑序来描述有一定前途。拓扑序也反而是二维相比三维的限制更多。

3.8、离散和连续

很多问题上，离散化和连续化是可以双向转变的。它们也都可以有或没有方向（序关系）。

实数是连续的，整数是离散的。

微积分是连续的，群一般是离散的。

拓扑可以连续也可以离散。注意集合元素，可以有方向或度量。

当然，我们甚至也可以把进制看成某种层次化的对称性。比如十进制就是在个十百千万……位上有不同的周期。进一步的抽象，我们甚至能把对数或p进数看成不同层次有不同对称性的特例，是有不同粒度的群组合。

当我们度量时也有离散和连续。既有拓扑不变量，也有熵这种介于离散和连续之间的量。甚至分形进一步模糊了其中的界限。

3.9、思考题

在谈了这么多几何和函数关系之后，再留一些思考题：

不确定性原理也可以看成真实数据在高维，而在低维时因为模型能力不足，只能看到某个侧面。这就像双目竞争。当然，也可以假想有超过两个量的不确定性关系，只不过其中的线性无关量是在更低的维度。这种思考方式也可能带来新的物理学。

作为拓扑的类似物，只保留序关系、不保留距离的数学会有什么性质？

传统的世界逐渐升维，那有没有只有高维，却没有低维的世界？

在这个世界的我们从二维、三维开始想象高维，其他维度生物的想象力又该如何伸缩？

我们在这个宇宙先发展出微积分后有群论。另一个世界先有群论的话，是什么样，又会怎么发展？

4、通天塔

做了这么多铺垫，让我们回到现实世界，看一看那些公理、定理、数学常数、以及数学知识点自何而来。

4.1、公理

欧式几何有如下一些基础：

①、几何公理：直线公理、延长公理、圆公理、直角公理、平行公理（第五公设）；

②、一般公理：等量代换、等量加法、等量减法、移形叠合公理、全量大于分量公理；

③、定义：点没有部分、线段有长度没宽度、也没面积、直线是点组成的、面积有长宽、面积的极端是线。

其中，直线公理和延长公理，说的是单维度的相等、不等和序关系；圆公理和直角公理，说的是维度为2时的函数性质；一般公理全部是函数性质及其自洽性；定义全部是不同维度下的函数。经过我们第三章的拆解，现在可以发现欧几里得的表述极为冗余，而我们前面的表述除了简介更可以扩展到更广阔不同可能性的宇宙之中。

平行、垂直，逻辑的与或非，基于公理的各种定理在这个框架下都可以被完全解构了。

不过这里值得提到的一点是，作为代数体系中最小核心组合的公理，是不唯一的。就像从1+2=3可以得知3-2=1，或者一组向量有最大线性无关组，我们有多种可能性来选择作为基础的公理组合，而它们也都是等效的。

这种等效性和小学应用题与代数的关系也很像。不使用代数也可解应用题，并且这个过程倒是有助于理清一种逻辑关系。当然，从代数的角度也能反演这个过程。它们作为一个整体，充实了正反演绎的对称性。

4.2、定理及其等价物

公理可以推出定理。那我们在小标题所说定理的等价物是什么？

请问圆周率π和自然对数e或者虚数i，是怎么来的？加载了别的代数体系的世界，会有这些相同的数吗？还是说那里并不一样？

1897年印第安纳州立法圆周率等于3.2，好家伙。这涉及到几何世界有多少的自主权，以及没有几何还会不会有圆周率。

好在，如我们前面所说，一切几何问题都可以找到一块代数的基石。π的本质是无穷级数。当然这也有级数收敛的问题。有多种不同无穷级数之间的等价问题，其中有些就收敛得特别快。

由拉马努金发现的那个，每多计算一项，就可以多出8位有效数字。

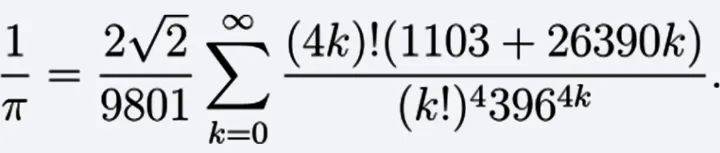
在代数世界，三角函数sin、cos自然也有对应的级数。

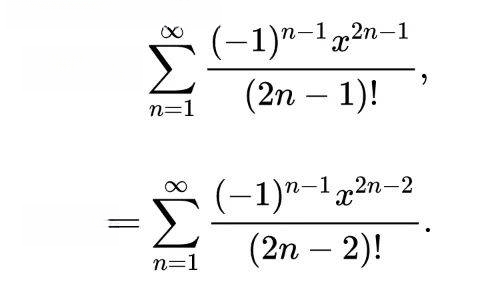
想反过来得到角度？反三角函数也不例外的有级数展开。

至于和角公式等三角公式，从几何直观的推导相比代数推导要容易许多。不过别忘了，这是因为我们所研究的几何世界，已经加载了一些代数结构，所以相当于扩展了原本的最小公理集合。在扩大的公理组上做推导那自然会容易了许多。

自然对数e也有极限定义和无穷级数展开的两种等价形式。

虚数i定义为-1的1/2次方。虽然说只要一个转换函数就可以代替，但因为其常用，就被独立成了一个新的概念。

我们也因此知道了在数学定理推导的时候，有很多步骤，为什么只有那最后一击得到的结果才是定理，而前面的都只能称为过程或引理。原因还是在于是否常用。

定理和上述这些（以及其他不包含于此的）数学常数，都是低层概念的高层整合。

需要注意的是，自洽的警告不断的回响。加入i扩大了我们的处理能力，便有人想能否有三元数？很可惜，我们只能有四元数、八元数和十六元数。其中哈密顿发现的四元数抛弃了交换律，从八元数开始又进一步丢掉了结合律。

如果要说一个在物理中的相关概念，那就是简并，即同一宏观态下有多个不同的精细状态。这又和复杂系统的分岔理论联系了起来。也许下一个什么节日我们有空再谈。

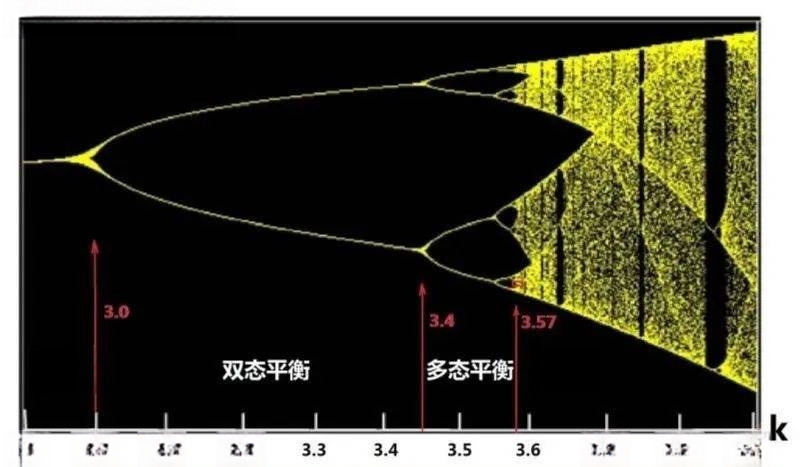
4.3、数学公式

该说的已经差不多了，我特地又去找了下小学和初中的数学知识大全。

三角形、长方形、平行四边形、梯形、正方形、圆的周长、面积；单位换算；交换律、结合律和分配率；方程；分数的加减乘除；全等和相似三角形；投影和对称；圆和点、线的关系；实数；多项式；方程；统计和概率。

它们无一不在前面的整个框架之下。知识点太多，聪明的读者朋友们，你们只需要忘记就能学会。

费曼说，如果只能把人类的科学史留下一句话，那就是一切东西都是由原子构成的。但古希腊也有原子论。这两个原子论恐怕只有字面的相似性。

大家早都知道数形结合，那今天追随你们的教员，一起重新思考过上面这些问题的小朋友大朋友们，是否有不一样的感悟呢？

我在此给你们颁发宇宙哲学家证书。也祝你们的未来，人类群星闪耀。

本文特别送给米和π。