中

考

数

学

进入初三之后，中考升学的问题将面对面的呈现到学生眼前，因此，每一个学生都希望自己有着更充足的准备、领先他人一步进入初三。想要领先他人一步进，那就得利用好暑假，对之前所学的进行复习总结，对即将要学习的进行有计划的预习学习。今天，老师和大家分享的是2025中考数学 | 几何模型专题复习：全等模型——角平分线模型！

模型一、角平分线垂中间（角平分线+内垂直）

【模型解读与图示】

条件：如图1，OC为∠AOB的角平分线，AB⊥OC，

结论：△AOC≌△BOC，△OAB是等腰三角形、OC是三线合一等。

条件：如图2，BE为∠ABC的角平分线，BE⊥EC，延长BA，CE交于点F.

结论：△BEC≌△BEF，△BFC是等腰三角形、BE是三线合一等。

【例题】在△ABC中，AB=AC，∠BAC=90，BD平分∠ABC交AC于点D．

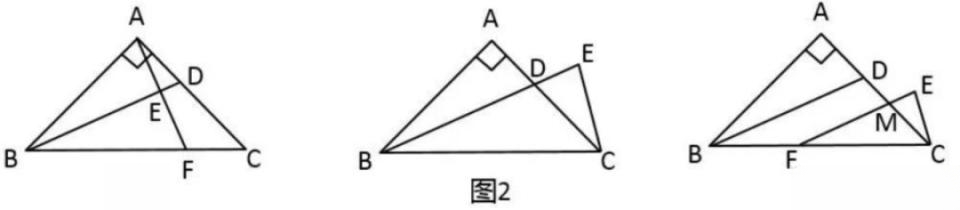
（1）如图1，点F为BC上一点，连接AF交BD于点E．若AB=BF，求证：BD垂直平分AF．

证明 ∵BD平分∠ABC，

∴∠ABE=∠FBE，

∵BA=BF，BE=BE，

∴△ABE≌△FBE（SAS），

∴AE=FE，∠AEB=∠FEB=1/2× 180°=90°，

∴BD垂直平分AF．

（2）如图2，CE⊥BD，垂足E在BD的延长线上．试判断线段CE和BD的数量关系，并说明理由．

解：BD=2CE，理由如下：延长CE，交BA的延长线于G，

∵CE⊥BD，∠ABE=∠FBE，

∴GE=2CE=2GE，

∵∠CED=90°=∠BAD，∠ADB=∠EDC，

∴∠ABD=∠GCA，

又AB=AC，∠BAD=∠CAG，，

∴△BAD≌△CAG（ASA），

∴BD=CG=2CE，

（3）如图3，点F为BC上一点，∠EFC=1/2∠ABC，CE⊥EF，垂足为E，EF与AC交于点M．直接写出线段CE与线段FM的数量关系．

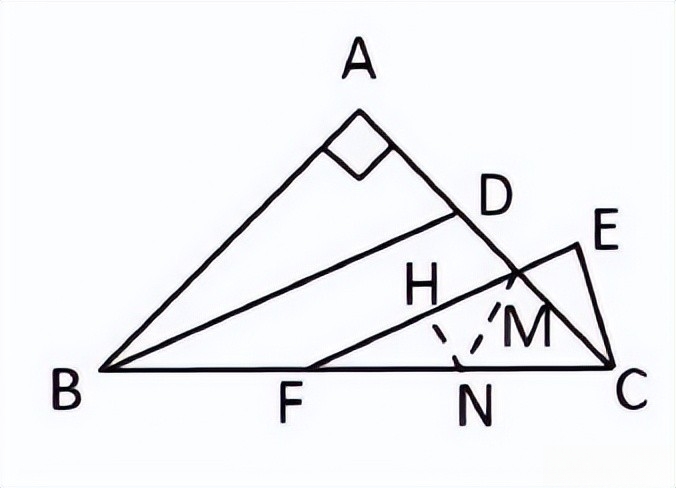
解：FM=2 CE，理由如下：作FM的中垂线NH交CF于N，交FM于H，

∴FN=MN，MH=FH=1/2FM，

∴∠NMH=∠NBH，

∵∠EFC=1/2∠ABC=22.5°，

∴∠MNC=2∠NFH=2×1/2∠ABC=∠ABC，

∵AB=AC，∠BAC=90，

∴∠ABC=∠ACB=∠MNC=45°，

∴NM=CM=FN，

∵∠EMC=∠MFC+∠MCF=22.5°+45°=67.5°，

∴∠ECM=90°-∠EMC=22.5°，

∴∠NFH=∠MCE，

又∵∠FHN=∠E=90°，

∴△FNH≌△CME（AAS），

∴FH=CE，

∴FM=2FH=2CE．

模型二、角平分线构造轴对称模型（角平分线+截线段相等）

【模型解读与图示】

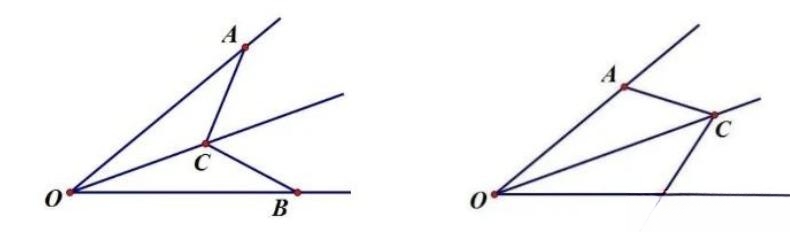
条件：如图，OC为∠AOB的角平分线，A为任意一点，在OB上截取OB=OA，连结CB.

结论：△OAC≌△OBC，CB=CA。

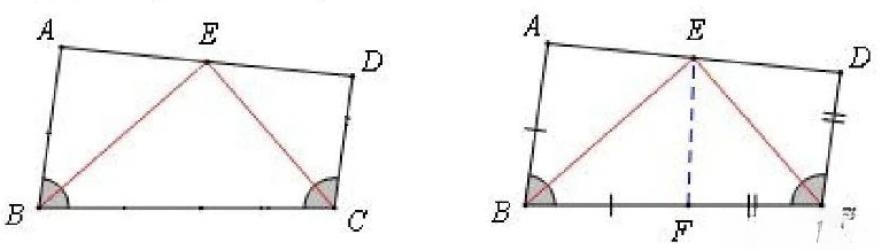
条件：如图，BE，CE分别为∠ABC和∠BCE的角平分线，AB∥CD，在BC上截取BF=AB，连结EF.

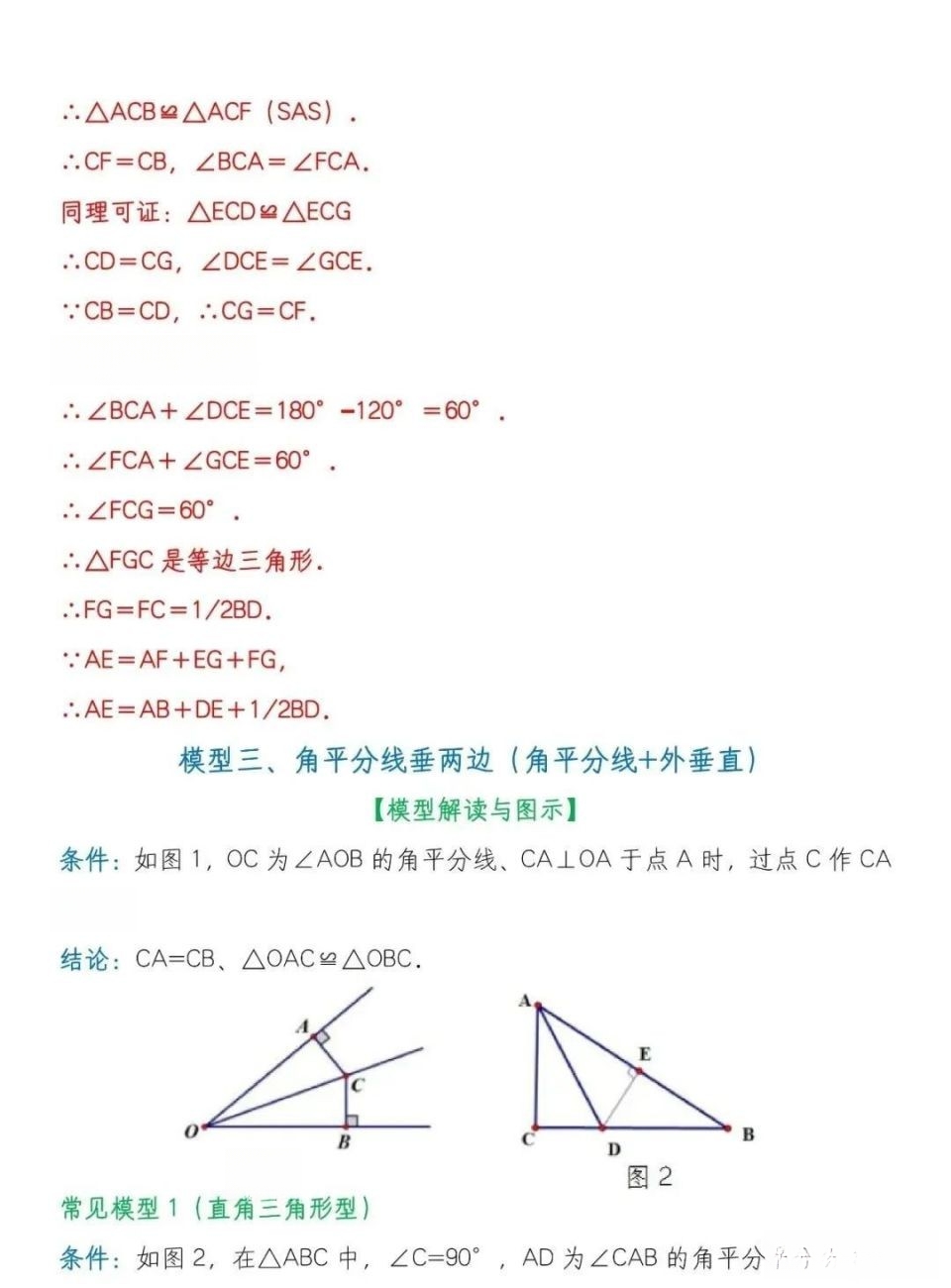
【例题】在四边形ABDE中，C是BD边的中点．

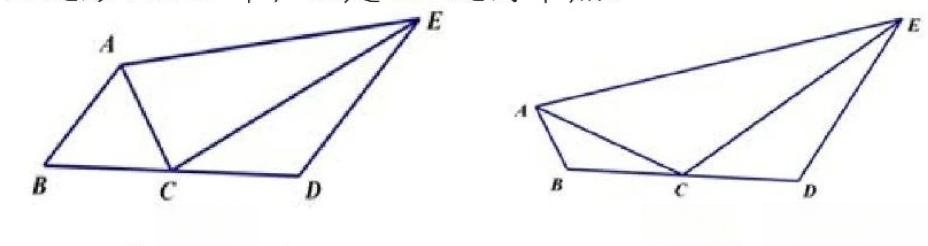
（1）如图（1），若AC平分∠BAE，∠ACE=90°，则线段AE、AB、DE的长度满足的数量关系为______；（直接写出答案）；

解：如图（1），在AE上取一点F，使AF＝AB．

∵AC平分∠BAE，

∴∠BAC＝∠FAC．在△ACB和△ACF中，

AB=AF，∠BAC＝∠FAC，AC=AC，

∴△ACB≌△ACF（SAS）．

∴BC＝FC，∠ACB＝∠ACF．

∵C是BD边的中点，

∴BC＝CD．∴CF＝CD．

∵∠ACE＝90°，

∴∠ACB＋∠DCE＝90°，∠ACF＋∠ECF＝90°．

∴∠ECF＝∠ECD．

在△CEF和△CED中，CF＝CD，∠ECF＝∠ECD，CE=CE，

∴△CEF≌△CED（SAS）．∴EF＝ED．

∵AE＝AF＋EF，

∴AE＝AB＋DE．

可直接保存图片打印